Murtolukujen sovellukset
Murtolukujen sovelluksilla tarkoitetaan sanallisia tehtäviä, joihin liittyy murtolukuja. Tehtävät voi yleensä ratkaista useammalla tavalla, mutta tehtävissä täytyy näkyä aina laskulauseke. Näihin tehtäviin kannattaa soveltaa samoja lähestymistekniikoita, jotka esiteltiin jo peruslaskutoimitusten yhteydessä:
1. Lue koko tehtävä.
2. Suunnittele ja ajattele. Mitä kysyttiin? Mitä tietoja annettiin?
3. Etsi, alleviivaa tai ympyröi tärkeät luvut.
4. Piirrä kuva, jos se auttaa sinua hahmottamaan tehtävän paremmin.
5. Päättele, mitä laskutoimituksia tarvitaan. Kirjoita laskutoimitukset näkyviin ja laske.
6. Tarkista ja kirjoita vastaus. Onko tulos järkevä? Onko tuloksen tarkkuus sopiva? Onko vastauksen yksikkö kirjoitettu näkyviin? Onko yksikkö oikein?
Esimerkkejä
Esim. 1. 32:sta opiskelijasta kahdeksasosa oli sairaana. Kuinka monta opiskelijaa oli paikalla?
${\frac{1}{8}\cdot32=4}$ sairaana
${32 − 4 = 28}$ paikalla
TAI
${\frac{32}{8}=4}$ sairaana
${32 − 4 = 28}$ paikalla
TAI
${\frac{7}{8}\cdot32=28}$ paikalla
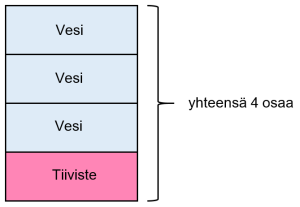
Esim. 2. Mehutiivisteen sekoitussuhde on 1 : 3 tiivistettä ja vettä. Kuinka paljon tiivistettä ja vettä tarvitaan, kun valmistetaan 8 litraa valmista mehua?
Piirretään kuva tilanteesta:
Tiivisteen määrä: ${\frac{1}{4}\cdot8\ l\ =\ 2\ l}$
TAI
Tiivisteen määrä: ${8\ l\ :\ 4\ =\ 2\ l}$
Veden määrä: ${\frac{3}{4}\cdot8\ l\ =\ 6\ l}$
TAI
Veden määrä: ${8\ l\ :\ 4\ \cdot\ 3=\ 6\ l}$
TAI
Veden määrä: ${8\ l\ -2\ l\ =6\ l}$