meta data for this page
Potenssi ja juuret
Potenssi
Potenssilaskuihin liittyvät käsitteet kantaluku ja eksponentti. Potenssilasku muuttuu kertolaskuksi niin, että kantaluku kerrotaan itsellään niin monta kertaa kuin eksponentti osoittaa.
Esim.
${6^3=6\cdot6\cdot6=216}$
Tässä esimerkissä kantaluku on 6 ja eksponentti on 3.
Esimerkkejä
Kirjoita potenssilaskut kertolaskuna ja laske.
${8^2=8\cdot8=64}$
${2^6=2\cdot2\cdot2\cdot2\cdot2\cdot2=64}$
Kirjoita potenssilasku kertolaskuna.
${x^4=x\cdot x\cdot x\cdot x}$. Tämän tehtävän vastausta ei voida laskea, koska ei tiedetä ${x}$:n suuruutta. Vastaus on yleensä selkeämpi antaa potenssilaskuna eli ${x^4}$.
Negatiivinen kantaluku:
${\left(-3\right)^4=-3\cdot\left(-3\right)\cdot\left(-3\right)\cdot\left(-3\right)=81}$
${\left(-6\right)^5=-6\cdot\left(-6\right)\cdot\left(-6\right)\cdot\left(-6\right)\cdot\left(-6\right)=-7776}$
Kantaluku on kummassakin tehtävässä negatiivinen. Kun eksponentti on parillinen (2, 4, 6, …), vastaus on positiivinen. Kun eksponentti on pariton (1, 3, 5, …), vastaus on negatiivinen.
Kun potenssilasku kirjoitetaan auki kertolaskuna ja kantaluku on negatiivinen, täytyy käyttää sulkuja. Termit täytyy laittaa sulkuihin toisesta termistä alkaen, koska kerto- ja miinusmerkiä ei saa kirjoittaa suoraan peräikkäin.
Seuraavassa esimerkissä miinus ei ole osa kantalukua:
${-5^4=-5\cdot5\cdot5\cdot5=-625}$
Eksponenttina 1 tai 0
Kun eksponenttina on 1, vastaus on kantaluku.
Esim. ${9^1=9}$ tai ${15^1=15}$
Kun eksponenttina on 0, vastaus on aina 1.
Esim. ${7^0=1}$ tai ${13^0=1}$
Neliö ja kuutio
Eksponenttiä 2 sanotaan usein neliöksi. Esim. luvun 7 neliö tarkoittaa laskutoimitusta ${7^2=49}$.
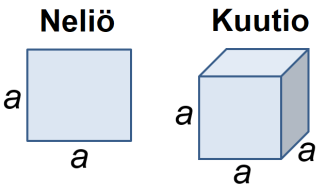
Eksponentin 2 nimitys neliö tulee neliön pinta-alan laskusta. Neliössä on neljä yhtä pitkää sivua ja neliön kaikkien kulmien suuruus on 90°. Neliön pinta-ala lasketaan sivun pituus · sivun pituus ja koska sivujen pituudet ovat neliössä samat voidaan laskea ${\left(sivun\ pituus\right)^2}$.
Eksponenttia 3 sanotaan usein kuutioksi. Esim. luvun 5 kuutio tarkoittaa laskutoimitusta ${5^3=125}$.
Kuutio on kolmiulotteinen kappale. Kuution kaikki sivut eli särmät ovat yhtä pitkiä ja kaikki kulmat ovat 90°. Kuution tilavuus lasketaan särmän pituus · särmän pituus · särmän pituus eli ${\left(särmän\ pituus\right)^3}$.
Juuret
Tavallisin juuri on neliöjuuri. Neliöjuuri on neliöön (eli toiseen potenssiin) korottamisen käänteinen laskutoimitus. Joitakin neliöjuuri voi laskea päässälaskuna, mutta usein tarvitaan avuksi laskinta. Neliöjuurta ei voi ottaa negatiivisesta luvusta.
Kuutiojuuri on kuutioon (eli kolmanteen potenssiin) korottamisen käänteinen laskutoimitus. Kuutiojuuri pystyy laskemaan päässälaskuna vain muutamia.
Esimerkkejä
Neliöjuuria:
${\sqrt{16}=4}$. Mieti, mikä luku potenssiin 2 on 16 eli ${x^2=16}$ → ${x=4}$
${\sqrt{81}=9}$. Mieti, mikä luku potenssiin 2 on 81 eli ${x^2=81}$ → ${x=9}$
${\sqrt{50}≈7,07}$. Tämä tehtävä täytyy laskea laskimella.
${\sqrt{-9}}$ ei ole ratkaisua. Jos minkä tahansa negatiivisen luvun korottaa toiseen potenssiin, vastaus on aina positiivinen. Neliöjuuren arvoa ei voida määrittää negatiivisista luvuista.
Kuutiojuuria:
${\sqrt[3]{27}=3}$. Mieti, mikä luku potenssiin 3 on 27 eli ${x^3=27}$ → ${x=3}$
${\sqrt[3]{125}=5}$. Mieti, mikä luku potenssiin 3 on 125 eli ${x^3=125}$ → ${x=5}$
${\sqrt[3]{-125}=-5}$. Kuutiojuuri voidaan ottaa myös negatiivisesta luvusta, koska ${(-5)^3=-125}$
${\sqrt[3]{95}≈4,56}$. Tämä tehtävä täytyy laskea laskimella.