meta data for this page
Suureet ja mittayksiköt
- Suure on jokin mitattava ominaisuus. Esim. pituus, massa (eli puhekielessä paino), pinta-ala ja tilavuus ovat suureita.
- Mittaluku on se luku, joka saadaan mittauksessa vastaukseksi. Mittaluku voi olla esim. 170, 3 tai 5,8.
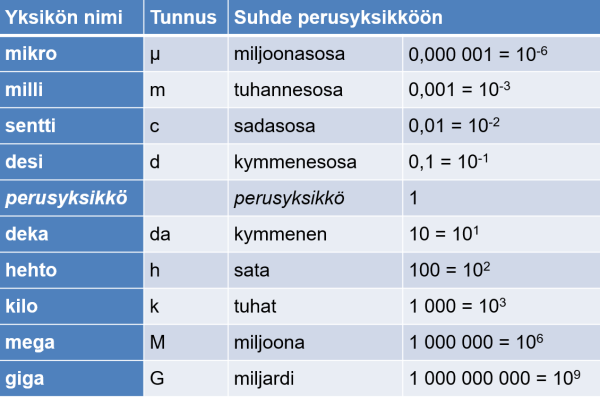
- Mittayksikkö ilmoitetaan mittaluvun yhteydessä. Mittayksikkö kertoo mittaluvun suuruusluokan, esim. 170 cm. Mittayksiköitä ovat mm. metri, kilogramma, neliömetri, kuutiometri ja litra. Jokaisella yksiköllä on lyhenne, joka koostuu yhdestä tai kahdesta kirjaimesta.
Mittayksiköissä on aina perusyksikkö kuten esim. metri tai litra.
Pituus, massa ja tilavuus litroina
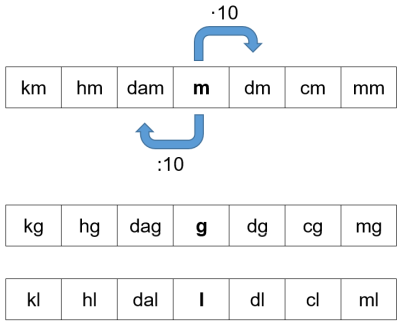
Pituuden ja massan suhdeluku on 10. Aina kun pituuden tai massan yksikköä muutetaan yhdellä luku kerrotaan tai jaetaan kymmenellä. Kun tilavuus ilmoitetaan litroina, myös sen suhdeluku on 10.
Esimerkkejä
${45\ mm=4{,}5\ cm=0{,}45\ dm=0{,}045\ m}$
${350\ m=35\ dam=3{,}5\ hm=0{,}35\ km}$
${750\ mg=7{,}5\ cg=0{,}75\ dg=0{,}075\ g}$
${3540\ g=354\ dag=35{,}4\ hg=3{,}54\ kg}$
${680\ ml=68\ cl=6{,}8\ dl=0{,}68\ }$
Pinta-ala
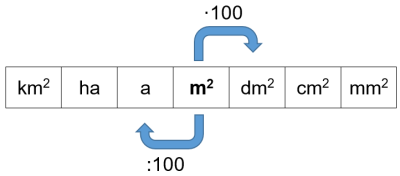
Pinta-alat ilmoitetaan neliömetreinä, ${m^2}$. Pinta-alojen suhdeluku on 100 eli kun pinta-alan yksikkö muuttuu yhdellä, pinta-alan lukuarvoa kerrotaan tai jaetaan sadalla. Neliöhehtometrin sijaan käytetään termiä hehtaari, ha, ja neliödekametrin sijaan termiä aari, a. Kaikissa muissa pinta-alan yksiköissä, paitsi hehtaarissa ja aarissa, näkyy metrin eksponenttina luku 2. Arjessa käytetään eniten pinta-alan yksikköjä ${m^2}$, ${a}$ ja ${ha}$.
Esimerkkejä
${350\ m^2=3{,}5\ a}$
${22500\ m^2=2{,}25\ ha}$
${0{,}03\ km^2=30 000\ m^2}$
${0{,}75\ m^2=7 500\ cm^2}$
${0{,}09\ dm^2=9\ cm^2}$
${365 000\ mm^2=0{,}365\ m^2}$
Tilavuus kuutioina
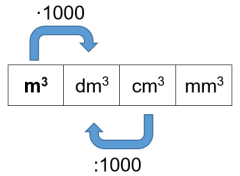
Tilavuudet voidaan ilmoittaa litroina tai kuutiometreinä, ${m^3}$. Kun tilavuudet ilmoitetaan kuutiometreinä, suhdeluku on 1000. Kun tilavuus kuutioina muuttuu yhdellä, luku kerrotaan tai jaetaan tuhannella.
Yksi kuutio, ${m^3}$, on jo niin suuri yksikkö, että suurempien yksiköiden käytölle ei ole tarvetta.
Esimerkkejä
${25\ cm^3=25\ 000\ mm^3}$
${0{,}010\ m^3=10\ dm^3}$
${125\ 000\ cm^3=0{,}125\ m^3}$
Kuutioiden ja litrojen yhteys
Tilavuusissa kuutioina ja litroina on kolme vastaavuutta, jotka täytyy muistaa ulkoa:
- ${1\ ml=1\ cm^3}$
- ${1\ l=1\ dm^3}$
- ${1\ 000\ l=1\ m^3}$
Kun kuutioita ja litroja muunnetaan toisikseen, muunnokset tehdään yllä olevien vastaavuuksien kautta.
Esimerkkejä
${15\ dm^3=15\ l}$
${35\ dl=3{,}5\ l=3{,}5\ dm^3=0{,}0035\ m^3}$
${0{,}07\ m^3=70\ dm^3=70\ l}$
${5000\ mm^3=5\ cm^2=5\ ml}$
Ajan muunnokset
Ajan muunnokset ovat arkipäiväisiä, mutta silti haastavia, koska
- 1 min = 60 s
- 1 h = 60 min = 60 · 60 s = 3600 s
Lisäksi täytyy muistaa, että
- yksi vuorokausi, 1 d = 24 h
- yksi vuosi, 1 a = 365 d
Vuorokaudesta käytetään myös merkintää vrk.
Esimerkkejä
${3{,}5\ h=3{,}5\ h\ \cdot60\ \frac{\min}{h}=\ 210\ \min}$
$3000\ s =\frac{3000\ s}{60\ \frac{s}{\min}}=50\min$
${2{,}5\ d=2{,}5\ d\cdot24\ \frac{h}{d}=60\ h}$