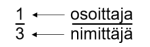Murtoluku muodostetaan kahden kokonaisluvun osamääränä eli jakolaskuna. Esim. ${\frac{1}{3}}$ ja $\frac{5}{6}$ ovat murtolukuja. Murtoluku voidaan aina muuntaa tarvittaessa desimaaliluvuksi.

Murtolukuihin liittyviä käsitteitä ovat osoittaja, nimittäjä, murtoluku ja sekaluku. Kun murtolukua muutetaan erinäköiseksi puhutaan laventamisesta ja supistamisesta. Laventamisessa ja supistamisessa murtoluvun suuruus ei muutu.

Murtoluvun yläosaa eli jaettavaa kutsutaan osoittajaksi ja alaosaa eli jakajaa nimittäjäksi

Murtoluvut voidaan luokitella edelleen murtoluvuiksi ja sekaluvuiksi. Joskus käytetään erikseen termiä epämurtoluku, jos murtoluvun osoittaja on suurempi kuin nimittäjä.

Sekalukuja ovat esim. ${2\frac{5}{6}}$, ${1\frac{3}{4}}$ ja ${-3\frac{1}{8}}$.

Murtolukuja ovat esim. ${\frac{1}{3}}$, ${\frac{2}{5}}$, ${\frac{15}{7}}$ ja ${\frac{12}{5}}$.

Murtoluvuista ${\frac{15}{7}}$ ja ${\frac{12}{5}}$ voidaan käyttää myös termiä epämurtoluku.

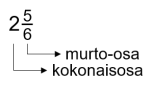
Sekaluku koostuu kokonaisosasta ja murto-osasta.

Murtolukujen laskutoimituksissa pitää osata muuttaa sekalukuja murtoluvuiksi ja toisinpäin. Jopa arjessa tulee tilanteita, joissa täytyy ymmärtää mikä murtoluku ja desimaaliluku vastaavat toisiaan.

Esimerkkejä.

${2\frac{5}{6}=\frac{2\cdot6+5}{6}=\frac{17}{6}}$

${1\frac{2}{3}=\frac{1\cdot3+2}{3}=\frac{5}{3}}$

${-7\frac{4}{5}=-\frac{7\cdot5+4}{5}=-\frac{39}{5}}$

${3=\frac{3}{1}}$. Luvun 1 voi aina lisätä nimittäjään.

Toisaalta esim. ${2\frac{5}{6}}$ muuttamisen voi ajatella niin, että 2 kokonaista on ${\frac{12}{6}}$, josta edelleen ${\frac{12}{6}}$ + ${\frac{5}{6}}$ =${\frac{17}{6}}$

Kun murtoluku muutetaan sekaluvuksi, täytyy suorittaa murtoluvun jakolasku. Kokonaisosa saadaan jakolaskusta ja tämän jälkeen selvitetään, mikä luku jää osoittajaan.

Esimerkki.

${\frac{24}{5}=4\frac{4}{5}}$ Mieti: ${\frac{20}{5}=4}$ ja ${\frac{25}{5}=5}$ eli kokonaisia 4. 4 kokonaista vastaa ${\frac{20}{5}}$, joten ${24-20=4}$ eli murto-osa on ${\frac{4}{5}}$

Tavallisimmat murtoluvut pitää osata muuttaa desimaaliluvuiksi suoraan tai pienen päättelyn kautta. Hankalammat murtoluvut on helpointa muuttaa desimaaliluvuksi laskimella.

Esimerkkejä helpoista muunnoksista, jotka täytyy osata ilman laskinta:

${\frac{1}{10}=0,1}$. Kymmenesosa kokonaisesta.

${\frac{1}{3}=0,333}$. Kolmasosa eli 33,3 %.

${\frac{2}{3}=0,666}$. Kaksi kolmasosaa. Koska kolmasosa on 33,3 %, on kaksi kolmsaosaa 2 · 33,3 % = 66,6 %.

${\frac{9}{10}=0,9}$. ${\frac{1}{10}=0,1}$. ${\frac{9}{10}}$ on 1 − 0,1 = 0,9.

Esimerkiksi ${\frac{9}{13}}$ muuttaminen ei onnistu helposti, joten se tehdään laskimella. Laskimeen näpytellään 9 : 13, ja laskin antaa tulokseksi 0,8181…

Sekaluvun muuntamisessa desimaaliluvuksi muutetaan vain murto-osa. Kokonaisosa kirjoitetaan suoraan luvun alkuun, ennen pilkkua.

Esim. ${2\frac{5}{6}=2,833}$. Vain ${\frac{5}{6}}$ muutetaan murtoluvuksi päättelemällä tai laskimella. ”2,” kirjoitetaan suoraan luvun alkuun.

Desimaaliluvusta lasketaan pilkun jälkeisten numeroiden lukumäärä.
Jos pilkun jälkeen on yksi numero (eli kymmenesosia), murtoluvun nimittäjäksi tulee luku 10.
Jos pilkun jälkeen on kaksi numeroa (eli sadasosia), murtoluvun nimittäjäksi tulee luku 100.
Luvun desimaaliosa merkitään osoittajaan.

Esimerkkejä.

${0,7=\frac{7}{10}}$

${0,21=\frac{21}{100}}$

${0,199=\frac{199}{1000}}$

Desimaaliluvun kokonaisosa on sama kuin murtoluvun kokonaisosa.

Esimerkkejä.

${2,7=2\frac{7}{10}}$

${-5,41=-5\frac{41}{100}}$

Murtoluvun supistaminen ja laventaminen muuttavat murtoluvun eri näköiseksi, mutta murtoluvun suuruus ei muutu. Esim. ${\frac{1}{2}=\frac{2}{4}}$. Laventaminen tarkoittaa murtoluvun osoittajan ja nimittäjän kertomista samalla luvulla. Supistaminen tarkoittaa murtoluvun osoittajan ja nimittäjän jakamista samalla luvulla. Jos katsotaan esimerkkiä ${\frac{1}{2}=\frac{2}{4}}$ vasemmalta oikealle, kyse on laventamisesta. Sekä osoittaja että nimittäjä on kerrottu luvulla 2. Jos katsotaan samaa esimerkkiä oikealta vasemmalle eli ${\frac{2}{4}=\frac{1}{2}}$ kyse on supistamisesta. Sekä osoittaja että nimittäjä on jaettu luvulla 2.

Laventaminen merkitään yläindeksillä murtoluvun vasemmalle puolelle (laventaminen, ”left”). Supistaminen merkitään yläindeksillä murtoluvun oikealle puolelle. Koska laventaminen ja supistaminen eivät muuta luvun suuruutta, kokonaisosa ei muutu.

Esim. Merkinnät.

Laventaminen ${^{2\text{)}}\frac{1}{5}=\frac{2\cdot1}{2\cdot5}=\frac{2}{10}}$

Supistaminen ${\frac{5}{20}^{\text{(}5}=\frac{\frac{5}{5}}{\frac{20}{5}}=\frac{1}{4}}$

Laventamista tehdään yleensä silloin, kun kaksi murtolukua täytyy saada samannimisiksi eli kummankin nimittäjään pitää saada sama luku. Supistamista käytetään mm. siihen, että muutetaan tehtävän vastaus lopulliseen muotoon. Lopullinen muoto on aina sellainen, jossa murto-osan osoittajassa ja nimittäjässä ovat mahdollisimman pienet kokonaisluvut.

6. Murtoluvut, tehtäviä