Sisällysluettelo
Peruslaskutaidot, tehtävät
1. Kymmenjärjestelmä, tehtäviä
- Minkä lukuyksikön paikalla luvussa 851039,746 on
- 1
- 3
- 4
- 8
- Muodosta viisinumeroinen luku, jossa on
- 1 satojen kohdalla
- 3 tuhansien kohdalla
- 6 ykkösten kohdalla
- 3 sadasosien kohdalla
- Kirjoita desimaalilukuna.
- kymmeniä 5, ykkösiä 3, kymmenesosia 7
- 4 ykköstä, 25 sadasosaa
- kymmeniä 3 ja 86 tuhannesosaa
- 0 kokonaista ja 21 kymmenestuhannesosaa
- 12 kokonaista 14 miljoonasosaa
- Valitse luvuista ne, jotka toteuttavat ehdon.
| a. Kymmeniä on 1, sadasosia on 8 | |||||
| 830,18 | 6710,38 | 184,21 | 217,008 | 315,580 | 3810 |
| b. Satoja on 7, kymmenesosia on 2. | |||||
| 700,35 | 1370,24 | 1750,25 | 75,2 | 753,21 | 725,02 |
| c. Ykkösiä on 3, kymmenesosia on nolla. | |||||
| 453,025 | 300,00 | 243,50 | 753,0 | 73,10 | 513,0 |
2. Lukujen suuruusvertailu, tehtävät
- Merkitse <, > tai = lukujen väliin.
- 1,03 _____ –1,03
- 0,05 _____ –1,05
- 2,74 _____ 2,8
- –6,24 _____ –6,3
- –7,05_____ –7,5
- –0,3 _____ –0,03
- Järjestä luvut suuruusjärjestykseen:
| 0,5 | 0,1 | 0,01 | 0,2 | 0,4 | 0,15 |
_____ < _____ < _____ < _____ < _____ < _____
| 0,99 | 0,11 | 1,0 | 0,45 | 1,1 | 0,5 |
_____ < _____ < _____ < _____ < _____ < _____
| 5,05 | 5 | 5,15 | 0,05 | 5,5 | 0,55 |
_____ < _____ < _____ < _____ < _____ < _____
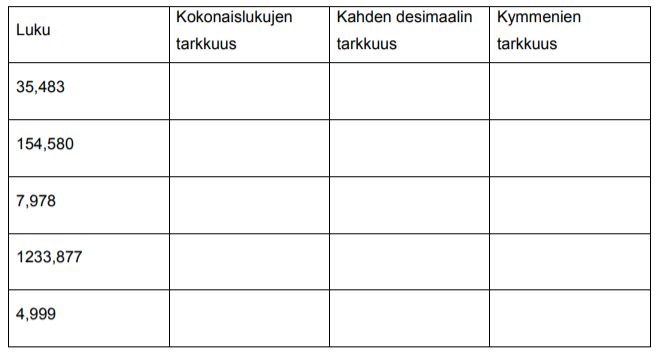
3. Luvun tarkkuus, likiarvot ja pyöristäminen, tehtävät
- Kuinka monta merkitsevää numeroa luvussa on?
- 4568,2
- 3055
- 500
- 63,050
- 0,470
- 450,50
- Pyöristä alla olevat luvut kolmen merkitsevän numeron tarkkuudella.
- 0,5432
- 505,59
- 54351
- Laske ja ilmoita tulos oikealla tarkkuudella.
- 14,53 kg + 37 kg + 1,9 kg + 0,025 kg =
- 0,25 m + 12,8 m – 10 m + 4,209 m =
- 2500 km + 439 km + 9200 km =
- 88 € + 42,04 € + 187,20 € - (100 € + 55,01 €) =
- 4,2 m ∙ 3,6 m =
- 7,25 m ∙ 4,02 m ∙ 3,1 m =
- 0,28 ∙ 728 g =
- 15,96 m : 4 =
4. Peruslaskutoimitukset, tehtäviä
- Merkitse ja laske
- Lukujen 14 ja 5 summa.
- Lukujen -8 ja 3 tulo.
- Lukujen 20 ja -5 erotus.
- Vähenevä on 15 ja vähentäjä on 10.
- Jaettava on 35 ja jakaja on 7.
- Laske
- 51 ∙ 10 =
- 3,1 ∙ 10 =
- 12 ∙ 100 =
- 42,58 ∙ 100 =
- 0,34 ∙ 100 =
- −12,5 ∙ 100 =
- 16 ∙ 1000 =
- −141 ∙ 1000 =
- 23,5 ∙ 1000 =
- 0,41 ∙ 1000 =
- 50 : 10 =
- −351 : 10 =
- −5 : 10 =
- 0,45 : (−10) =
- 510 : 100 =
- −35 : 100 =
- 0,05 : 100 =
- 7500 : (−1000) =
- 78 : 1000 =
- 45,85 : 1000 =
- Laske.
- 5000 − 2 · 1000 =
- (5000 − 2) · 1000 =
- 20 · 5 + 25 · 5 =
- 5 + 2 · 10 + 5 · 10 =
- 20 · (5 + 25) · 5 =
- (5 + 2) · 10 + 5 · 10 =
- (5 + 2) · (10 + 5) · 10 =
- 2 · (5 + 2) · 10 + 5 · 10 =
- Laske.
- 5 + (−3) − 1 =
- −1 + (−3) − (−3) − (−1) + (+5) =
- −5 ∙ (−1) ∙ (−2) ∙ 3 ∙ (−2) =
- −30 : (−5) ∙ 2 ∙ (−2) =
- Laske. Merkitse myös välivaiheet.
- 150 : 50 ∙ 3 − (4 + 5)
=
=
= - (15 − 7) : 4 ∙ 6
=
=
= - 40 − 3 ∙ 12 + 120 : 5
=
=
= - (3 ∙ 2 − 15 : 3) : 4 + 1
=
=
= - 3 ∙ [5 + 2 ∙ (6 − 5)]
=
=
= - [18 + 15 − (4 − 2)] ∙ 3
=
=
= - 66 : {3 + [5 · (4+2)]}
=
=
= - 90 : (−15) − (− 48) : (−12)
=
=
= - $\frac{35-20}{2+3}$
=
= - $\frac{3 \cdot 5+8:2+5}{30:5 \cdot 3}$
=
=
=
5. Peruslaskutoimitusten sovellukset, tehtävät
1. Tarvitset koristenauhaa lasten askarteluryhmälle 35 m. Paljonko nauha maksaa, kun metrihinta on 3,40 €/m?
2. Mikä on kimallenauhan metrihinta, jos 15 m nauhaa maksaa 21,50 €? Anna vastaus kahden desimaalin tarkkuudella.
3. 450 g:n juustopala maksaa 4,95 €. Mikä on juuston kilohinta?
4. 0,35 litran oliiviöljypullo maksoi 3,29 €. Laske oliiviöljyn litrahinta.
5. Litra kahvia maksaa 1,50 €. Kuinka paljon maksaa 2 dl kupillinen?
6. Huoltoasemalle ostettiin 120 l öljyä. Monenko auton öljynvaihtoon se riitti, kun autoa kohti käytettiin öljyä 4,7 litraa?
7. Kuohuviinipullon tilavuus on 75 cl. Kuinka moneen kaatoon kuohuviini riittää, kun yksi kaato on 12 cl?
8. Parasetamolitabletin vahvuus on 500 mg. Potilaalle määrättiin 1000 mg parasetamaoli päivässä. Kuinka moneksi päiväksi riittää 30 kappaleen paketti?
9. Syöt 150 g purkin jogurttia. Jogurtti sisältää energiaa 113 kcal/100 g. Päivittäinen energiatarve on 2000 kcal. Kuinka monta purkkia jogurttia pitäisi syödä päivässä, jotta kaikki päivässä tarvittava energia tulisi vain jogurtista?
10. Työskentelit viikon aikana seuraavan taulukon mukaisesti. Tuntipalkkasi oli 12,72 €/h. Laske työtuntiesi määrä ja viikon palkkasi.
| Päivä | Työaika | Työtunnit |
|---|---|---|
| Ma | 7:30−15:00 | |
| Ti | 7:45−16:00 | |
| Ke | 8:00−15:45 | |
| To | 8:00−16:30 | |
| Pe | 7:45−16:15 | |
| Yhteensä | ||
11. Yhdysvaltojen dollarin kurssi on tällä hetkellä 1 € = 1,11 USD.
a. Laske kuinka paljon dollareita saat 250 eurolla.
b. Kuinka paljon 125 USD on euroina?
12. Bensiinin litrahinta on 1,497 €.
a. Kuinka paljon maksaa 45 litraa bensiiniä?
b. Kuinka monta litraa bensiiniä saa 30 eurolla?
13. Valopylväitä on tiellä 12 kappaletta (ensimmäinen heti tien alussa ja viimeinen tien lopussa). Kuinka pitkä tie on, kun kahden vierekkäisen valotolpan välinen etäisyys on aina 13 metriä?
14. Sähkönkulutus on vuodessa 2500 kWh. Sähkö maksaa keskimäärin (sähkö + siirtomaksu + kuukausimaksu) 13 snt/kWh. Kuinka paljon sähkölasku on kuukaudessa?
15. Tapahtuman aikuisten lippu maksoi 12 € ja lastenlippu 8 €. Tapahtumaan osallistui 75 aikuista ja 102 lasta. Tapahtuman kustannukset olivat 1150 €. Kuinka paljon järjestäjille jäi tapahtumasta voittoa?
16. Apple iPhone 7 Gt maksaa kertamaksulla 379,00 € tai 36 kk sopimuksella 10,52 €/kk. Tuleeko puhelimen osto halvemmaksi kertamaksulla vai 36 kk sopimuksella? Kuinka paljon hintaero on?
17. Kangaskassi maksaa 6,90 €. Kuinka monta kertaa kangaskassia täytyy käyttää, että sen ostaminen on kannattavampaa kuin kertakäyttöisten muovikassien osto. Muovikassi maksaa 15 snt.
18. Neljän hengen seurue aterioi ravintolassa. Pääruuat maksoivat yhteensä 72 €, jälkiruuat 4,5 €/hlö ja juomat yhteensä 12 €. Lasku jaettiin neljään yhtä suureen osaan. Kuinka paljon jokainen joutui maksamaan?
19. 15 tyttöä oli tulossa säbäturnauksesta ja he pysähtyivät ABC:lle syömään lounasta. Lounas maksoi koko joukkueelta 140 €. Kuinka paljon lounas maksoi yhdeltä henkilöltä?
6. Murtoluvut, tehtäviä
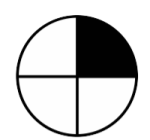
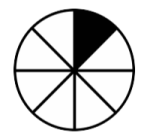
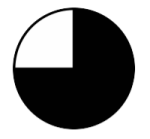
- Ilmoita mustan osan suuruus koko kuvasta murtolukuna.
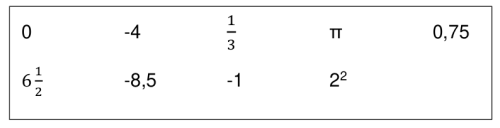
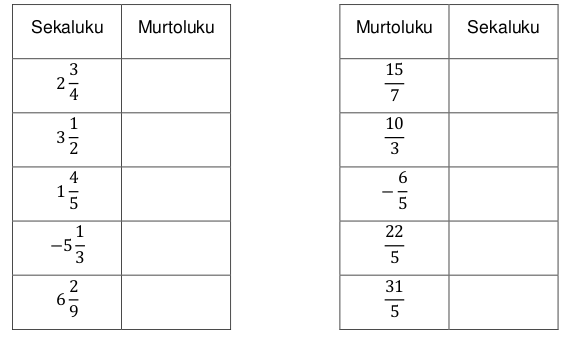
- Muunna murtoluvut desimaaliluvuiksi.
- $\frac{1}{4}$
- $\frac{2}{10}$
- $\frac{3}{5}$
- $\frac{21}{40}$
- $5 \frac{1}{4}$
- $2 \frac{11}{12}$
- $-4 \frac{13}{15}$
- Muunna desimaalit murtoluvuiksi.
- 0,2
- 0,81
- 0,25
- 1,3
- 5,321
- 2,9
- 12,31
- Lavenna murtoluvut annetulla luvulla.
- $^{5\text{)}}\frac{1}{2}$
- $^{4\text{)}}\frac{2}{3}$
- $^{3\text{)}}\frac{1}{4}$
- $^{2\text{)}}\frac{3}{5}$
- $^{6\text{)}}\frac{5}{6}$
- $^{2\text{)}}\frac{2}{9}$
- $^{9\text{)}}\frac{1}{3}$
- $^{2\text{)}}\frac{4}{7}$
- Supista murtoluvut mahdollisimman yksinkertaiseen muotoon. Merkitse näkyviin luku, jolla supistat.
- $\frac{3}{6}^{\text{(}}$
- $\frac{28}{7}^{\text{(}}$
- $\frac{15}{36}^{\text{(}}$
- $\frac{32}{72}^{\text{(}}$
- $\frac{112}{156}^{\text{(}}$
- $4 \frac{4}{28}^{\text{(}}$
- $2 \frac{5}{50}^{\text{(}}$
- $7 \frac{6}{36}^{\text{(}}$
7. Murtolukujen peruslaskutoimitukset, tehtäviä
- Laske. Supista vastaukset jos voit.
- $\frac{1}{4}+\frac{2}{4}=$
- $\frac{1}{3}+\frac{1}{3}=$
- $\frac{2}{5}+\frac{1}{5}=$
- $\frac{1}{4}+\frac{1}{4}=$
- $\frac{3}{4}-\frac{1}{4}=$
- $\frac{6}{6}-\frac{4}{6}=$
- $\frac{8}{9}-\frac{5}{9}=$
- $\frac{12}{15}-\frac{7}{15}=$
- Laske. Supista ja muuta vastaukset sekaluvuiksi, jos voit.
- $\frac{3}{5}+\frac{1}{3}=$
- $\frac{1}{2}+\frac{1}{4}=$
- $2+\frac{2}{3}=$
- $\frac{5}{5}-\frac{1}{4}=$
- $\frac{2}{3}-\frac{2}{7}=$
- $1-\frac{3}{8}=$
- $3\frac{3}{4}-\frac{1}{2}=$
- Laske.
- $2\frac{1}{7}+2\frac{2}{7}=$
- 1$\frac{1}{2}+\frac{3}{4}=$
- 1$\frac{2}{3}+2\frac{3}{8}=$
- 3$\frac{5}{6}+4\frac{2}{3}=$
- $2\frac{4}{5}-\frac{1}{3}=$
- $3-1\frac{1}{3}=$
- $1\frac{1}{4}-\frac{2}{3}=$
- $3\frac{2}{5}-2\frac{5}{6}=$
- Laske. Muist supistaa ja muuttaa vastaus tarvittaessa sekaluvuksi.
- $\frac{1}{4}\cdot\frac{3}{4}=$
- $\frac{1}{2}\cdot\frac{1}{2}=$
- $\frac{2}{5}\cdot\frac{1}{2}=$
- $\frac{2}{3}\cdot\frac{3}{4}=$
- $2\frac{3}{5}\cdot\frac{1}{2}=$
- $2\cdot\frac{4}{6}=$
- $\frac{1}{3}\cdot3=$
- $\frac{5}{6}\cdot\frac{3}{10}=$
- $2\frac{1}{5}\cdot3\frac{1}{2}=$
- $1\frac{3}{8}\cdot2\frac{1}{3}=$
- $2\frac{1}{4}\cdot4\frac{5}{6}=$
- Merkitse lukujen käänteisluvut.
- $\frac{2}{5}$
- $\frac{3}{8}$
- $\frac{1}{4}$
- $\frac{1}{6}$
- $5$
- $3$
- $4\frac{2}{3}$
- $2\frac{1}{4}$
- Laske.
- $\frac{3}{4}:\frac{1}{3}=$
- $\frac{4}{5}:\frac{1}{2}=$
- $\frac{3}{10}:\frac{3}{4}=$
- $\frac{5}{6}:\frac{1}{5}=$
- $1\frac{3}{7}:\frac{2}{5}=$
- $4:\frac{1}{5}=$
- $5\frac{3}{4}:1\frac{1}{2}=$
- $4\frac{2}{3}:2\frac{2}{3}=$
- Laske.
- $2\frac{4}{5}-\frac{1}{3}\cdot\frac{5}{8}=$
- $2:\frac{1}{5}\cdot\frac{2}{7}=$
8. Murtolukujen sovellukset, tehtäviä
Muista kirjoittaa kaikissa tehtävissä laskulausekkeet näkyviin.
- Eerolle, Timolle ja Juhanille maksetaan työstä yhteensä 250 €. Eero, Timo ja Juhani jakavat rahat tasan. Kuinka paljon kukin heistä saa?
- Omenoita oli alun perin 45 kpl. Omenoista on jäljellä $\frac{1}{3}$ . Kuinka monta omenaa on jäljellä?
- Raisan palkka on 3448 € ja siitä menee veroihin $\frac{1}{4}$ . Kuinka paljon Raisalle jää palkasta käteen?
- Paavo osti auton 11 000 eurolla. Vuoden kuluttua auton hinnasta oli jäljellä $\frac{3}{4}$ . Mikä auton arvo oli tällöin?
- Alun perin paita maksoi 24 €. Paidan hintaa alennettiin $\frac{2}{5}$. Kuinka monta euroa paita maksoi alennuksen jälkeen?
- Italiansalaatti maksoi 0,99 €. Italiansalaatin hintaa nostettiin $\frac{1}{3}$. Kuinka paljon italiansalaatti maksoi hinnan korotuksen jälkeen?
- Pesuainetiivistettä ja vettä sekoitetaan ohjeen mukaan suhteessa 1:9.
- Kuinka paljon vettä lisätään, jos pesuainetiivistettä käytetään 1,2 dl?
- Kuinka paljon valmista pesuainetta saadaan a-kohdassa?
- Kuinka paljon tiivistettä laitetaan 15 litraan vettä?
- Tiina söi $\frac{1}{4}$ pizzasta ja Aliisa söi $\frac{2}{3}$ pizzasta. Kuinka paljon pizzasta jäi Jarille?
- Ville söi karkeista viidesosan ja Kalle kaksi kolmasosaa. Muille jäi 44 karkkia. Kuinka monta karkkia söi Ville ja Kalle?
- Kalle syö karkeista puolet. Tiina syö jäljelle jääneistä karkeista puolet. Rasiaan jää 7 karkkia. Kuinka monta karkkia oli alun perin? Piirrä kuva.
- Matin viikkoraha on 20 €. Hän säästää rahasta $\frac{3}{4}$ polkupyörään. Pyörä maksaa 315 €. Kuinka monta viikkoa Matin täytyy säästää pyörään?
- Heikki, Jaana ja Ronja ostivat yhteensä 1500 kappaletta erikoisnappeja. Nappierä haluttiin jakaa tasan sen mukaan, kuinka paljon kukin oli maksanut. Heikki maksoi 90 €, Jaana 60 € ja Ronja 30 €. Kuinka paljon nappeja kukin sai?
9. Potenssi ja juuret, tehtävät
- Merkitse ja laske. Käytä tarvittaessa laskinta.
- Viisi potenssiin neljä.
- Kaksi potenssiin viisi.
- Luvun seitsemän neliö.
- Luvun kolme kuutio.
- Merkitse potenssilaskuna.
- $3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 =$
- $ 5 \cdot 5 \cdot 5$
- $-4 \cdot (-4) \cdot (-4) =$
- $-2 \cdot (-2) \cdot (-2) \cdot (-2)=$
- $x \cdot x \cdot x \cdot x =$
- $y \cdot y \cdot y \cdot y \cdot y \cdot y =$
- Merkitse kertolaskuna ja laske laskimella.
- $8^3 = $
- $5^7 = $
- $9^4 = $
- $6^4 = $
- $(-3)^5 = $
- $(-4)^6 = $
- Onko seuraavien tehtävien vastaus positiivinen (+) vai negatiivinen (−)? Tehtävä tehdään ilman laskinta.
- $(-4)^5=$
- $(-7)^{10}=$
- $(-254)^1=$
- $(-x)^{12}=$
- $(-16)^0=$
- $(-y)^9=$
- $-8^{12}=$
- $-41^{21}=$
- $(-1)^{2541}=$
- Laske ilman laskinta.
- $\sqrt{25} =$
- $\sqrt{16} =$
- $\sqrt{100} =$
- $\sqrt{36} =$
- $\sqrt{81} =$
- $\sqrt{1} =$
- $\sqrt[3]{1000} =$
- $\sqrt[3]{8} =$
- $\sqrt[3]{1} =$
- $\sqrt{-36} =$
- $\sqrt[3]{-27} =$
- $\sqrt[3]{-1000} =$
- Laske laskimella. Ilmoita tulos kahden desimaalin tarkkuudella.
- $\sqrt{12} =$
- $\sqrt{63} =$
- $\sqrt{241} =$
- $\sqrt{-115} =$
- $\sqrt[3]{80} =$
- $\sqrt[3]{-205} =$
- Laske laskimella neliön pinta-ala, kun neliön sivun pituus on
- 4,5 cm
- 3,2 m
- 15,7 m
- Laske laskimella kuution tilavuus, kun kuution särmän pituus on
- 13 cm
- 1,2 m
10. Syventävää tietoa potensseista, tehtävät
Kurssin itsenäiset suorittajat Etelä-Pohjanmaan Opistossa: Tämä aihe on valinnainen. Tee nämä tehtävät, jos tavoittelet kurssista hyvää arvosanaa.
- Muuta luvut kymmenpotenssimuotoon.
- 5 000 000 000 =
- 300 000 =
- 70 000 000 =
- 0,000 04 =
- 0,005 =
- 0,000 000 000 2 =
- Muuta luvut kymmenpotenssimuotoon.
- 58 000 =
- 63 000 000 =
- 24 100 000 =
- 354 000 =
- 0,003 2 =
- 0,000 000 87 =
- 0,000 000 000 54 =
- 0,000 000 000 000 245 =
- Muuta luvut normaalimuotoon.
- $5 \cdot 10^8 = $
- $10^{12} = $
- $3,6 \cdot 10^9 = $
- $2,1 \cdot 10^4 = $
- $3 \cdot 10^{-8} = $
- $8 \cdot 10^{-6} = $
- $10^{-3} = $
- $2,4 \cdot 10^{-3} = $
- $5,24 \cdot 10^{-9} = $
- $4,12 \cdot 10^{-15} = $
- Ilmoita potenssilaskut positiivisen eksponentin avulla, murtolukuna ja desimaalilukuna.
| Positiivinen eksponentti | Murtoluku | Desimaaliluku | |
|---|---|---|---|
| $5^{-2}$ | = | = | = |
| $2^{-6}$ | = | = | = |
| $4^{-3}$ | = | = | = |
| $3^{-3}$ | = | = | = |
| $1^{-4}$ | = | = | = |
5. Laske ilman laskinta. Käytä potenssien laskusääntöjä. Merkitse välivaihe.
a. $2^3 \cdot 2^3 = $
b. $\frac{3^4}{3^2} = $
c. $(5 \cdot 10)^2 =$
d. $\frac{4^2}{2^5} =$
6. Ilmoita potenssilaskut yksinkertaisemmassa muodossa.
a. $\frac{x^6}{x^2} =$
b. $x^5 x^2 =$
c. $y^2 y^4 =$
d. $(xy)^2 =$
e. $(\frac{x}{y})^3=$
f. $\frac{y^4}{y^6}=$