Sisällysluettelo
Tilastolliset tunnusluvut
Taulukot ja graafiset esitykset antavat hyvän yleiskuvan jakaumasta, eli siitä kuinka tutkittavan muuttujan saamat havaintoarvot jakautuvat. Tulkinnan ja johtopäätöksen tueksi tarvitaan erilaisia tunnuslukuja tiivistämään tietoa. Yleisimmin käytettyjä tunnuslukuja ovat sijaintiluvut (esimerkiksi keskiarvo, mediaani ja moodi) sekä hajontaluvut (esimerkiksi keskihajonta).
Keskiarvo
Tyypillinen ja yleinen sijaintiluku on keskiarvo. Keskiarvon saamiseksi lasketaan yhteen kaikkien havaintojen mittausarvot ja jaetaan se havaintojen lukumäärällä. Olet saattanut törmätä keskiarvon laskemiseen koulujen todistusten keskiarvoissa.
Esim. 1. Tepolla oli peruskoulutodistuksessa seuraavat numerot:
8, 7, 8, 9, 6, 7, 5, 8, 7, 7, 6, 8, 7, 9 ja 7.
Lasketaan hänen keskiarvonsa:
$\overline{x}=\frac{8+7+8+9+6+7+5+8+7+7+6+8+7+9+7}{15}$
$\overline{x}=\frac{109}{15}=7{,}3$
Mediaani (Md)
Mediaani (merkataan Md) tarkoittaa suuruusjärjestykseen esitetyn aineiston keskimmäistä arvoa tai kahden keskimmäisen keskiarvoa. Mediaani jakaa aineiston kahteen yhtä suureen osaan.
Esim. 2. Jatketaan edellistä esimerkkiä ja määritetään Tepon peruskoulutodistuksen mediaani. Järjestetään aluksi peruskoulutodistuksen arvosanat suuruusjärjestykseen:
5, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9
Arvosanoja on yhteensä 15, joista keskimmäinen havainto on 7.
5, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9
Esim. 3. Mitä, jos Teppo saisikin yhden valinnaisaineen lisää todistukseen? Oletetaan valinnaisaineen arvosanan olevan 9, jolloin arvosanat suuruusjärjestyksessä ovat
5, 6, 6, 7, 7, 7, 7,7, 7,8, 8, 8, 8, 9, 9, 9
Nyt havaintoja on parillinen määrä (16), joten mediaani saadaan laskettua kahden keskimmäisen arvosanan keskiarvosta
$M_d=\frac{7+7}{2}=7$
Moodi (Mo)
Moodi (Mo) eli tyyppiarvo tarkoittaa sitä arvoa, jota aineistossa on eniten. Voidaan myös sanoa, että se on aineiston luokka, jolla on suurin frekvenssi. Jos kahdella luokalla tai arvolla on yhtä suuret frekvenssit, voi moodeja olla useampia. Moodi on myös ainoa keskiluku, jota voidaan käyttää luokitteluasteikon muuttujalle, koska asteikon muuttujan havainnoilla ei ole keskinäistä järjestystä.
Esim. 4. Tarkastellaan Tepon päättötodistuksen arvosanoja, ja selvitetään mitä arvosanoja hänellä on eniten. Yksi tapa on laatia taulukko, johon listataan tiettyä havainnon arvoa vastaavat frekvenssit, eli kuinka monta kappaletta tiettyjä arvosanoja Tepolla on.
| Arvosana | Frekvenssi (kappaleita) |
| 5 | 1 |
| 6 | 2 |
| 7 | 6 |
| 8 | 4 |
| 9 | 2 |
Taulukosta havaitaan, että Tepolla on eniten arvosanaa 7 (yhteensä kuusi kappaletta), jolloin hänen päättötodistuksen moodi on 7.
Vaihteluväli
Vaihteluväli tarkoittaa väliä, jonka sisällä havainnot ovat. Vaihteluvälin pituus (merkitään R-kirjaimella) saadaan, kun lasketaan suurimman ja pienimmän arvon erotus.
Esim. 5. Tepon päättötodistuksen arvosanoissa suurin arvo on 9 ja pienin 5. Tepon vaihteluvälin pituus on siis
$R = 9 - 5 = 4$
Keskihajonta
Alla olevissa kuvissa katkoviiva kuvastaa keskiarvoa. Pienessä hajonnassa havainnot keskittyvät keskiarvon ympärille, kun taas suuressa hajonnassa havainnot levittyvät kauemmas keskiarvosta.
Tärkeä hajonnan mitta on keskihajonta (merkitään s-kirjaimella), joka ilmaisee, kuinka paljon havaintoaineiston arvot keskimäärin poikkeavat sen aritmeettisesta keskiarvosta. Mitä suurempi keskihajonta on, sitä enemmän aineistossa on vaihtelua. Matemaattisesti muuttujan havaintoarvojen keskihajonta lasketaan kaavalla:
$s=\sqrt{\frac{poikkeamien\ neliöiden\ summa}{n-1}}=\sqrt{\frac{\Sigma\left(x_i-\overline{x}\right)^2}{n-1}}$
jossa $x_i$ on havaintoarvo, $\overline{x}$ havaintoarvojen keskiarvo ja n on havaintojen lukumäärä.
Keskihajonta voidaan laskea nopeasti ja tarkasti erilaisilla taulukkolaskentaohjelmilla tai tilastomatematiikan toimintoja sisältävällä laskimella. Keskihajonnan laskeminen onnistuu myös käsin, joskin se on hieman työläämpää. Tarkastellaan esimerkin avulla, kuinka keskihajonta voidaan laskeaa käsin.
Esim. 6. Valitaan aineistoksi Tepon arvosanoista tutkittavaksi vain 5, 6, 7, 7 ja 9. Lasketaan aluksi otoksen keskiarvo:
$\overline{x}=\frac{5+6+7+8+9}{5}=7$
Tiedämme nyt havaintojen keskiarvon (7) ja havaintojen lukumäärän (5). Lasketaan seuraavaksi taulukkoon poikkeamien neliöiden summa, eli havaintoarvon ja keskiarvon erotus korotettuna potenssiin kaksi:
| $x_i$ | $\left(x_i-\overline{x}\right)$ | $\left(x_i-\overline{x}\right)$ |
| 5 | $5 - 7 = - 2$ | $(-2)^2=4$ |
| 6 | $6 - 7 = - 1$ | $(-1)^2=1$ |
| 7 | $7-7=0$ | $0^2=0$ |
| 8 | $8-7=1$ | $1^2=1$ |
| 9 | $9-7=2$ | $2^2=4$ |
| $\Sigma =10$ |
Taulukosta saadaan viimeisestä sarakkeesta keskihajonnan kaavassa oleva poikkeamien neliöiden summa (10). Sijoitetaan kaikki tiedot keskihajonnan kaavaan:
$s=\sqrt{\frac{\Sigma\left(x_i-\overline{x}\right)^2}{n-1}}=\sqrt{\frac{10}{5-1}}=\sqrt{2{,}5}\approx1{,}58$
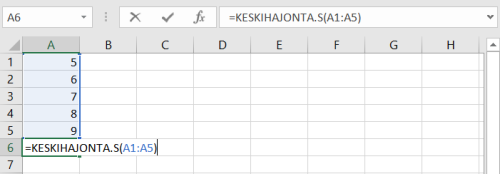
Toinen vaihtoehto on laskea suoraan esimerkiksi Excelillä. Sijoitetaan Exceliin havaintojen arvot ja komennolla =KESKIHAJONTA.S() voidaan valita solut, joista lasketaan keskihajonta.