Sisällysluettelo
Prosenttilaskennan tehtävät
Prosentti, tehtävät
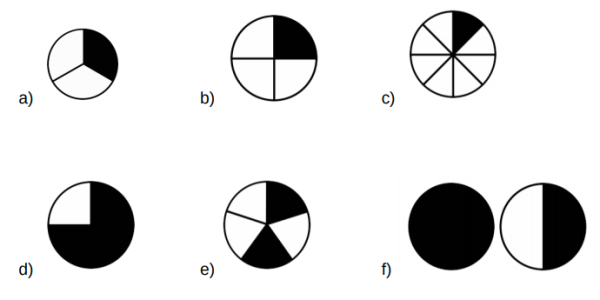
1. Merkitse mustan osuuden suuruus prosentteina.
2. Täydennä taulukko.
| Prosenttiluku | Murtoluku | Desimaaliluku |
|---|---|---|
| 1 % | ||
| $\frac{30}{100}$ | ||
| 0,09 | ||
| 15 % | ||
| $\frac{3}{100}$ | ||
| 0,005 | ||
| $\frac{2}{5}$ | ||
| 1,25 |
3. Laske tai päättele.
a) 1 % 300 eurosta.
b) 3 % 500 eurosta.
c) 25 % 600 eurosta.
d) 10 % 500 eurosta.
e) 30 % 250 eurosta.
f) 75 % 800 eurosta.
g) 90 % 60 eurosta.
4. Laske tai päättele. Kuinka monta prosenttia
a) 2 euroa on 20 eurosta?
b) 35 euroa on 70 eurosta?
c) 30 euroa 120 eurosta?
d) 90 euroa 120 eurosta?
e) 75 euroa 100 eurosta?
f) 180 euroa 200 eurosta?
g) 5 euroa 5000 eurosta?
5. Kuinka monta prosenttia on
a) puolet luvusta?
b) sadasosa luvusta?
c) kymmenesosa luvusta?
d) neljäsosa luvusta?
e) kaksi viidesosaa luvusta?
f) luku itse?
Muista kirjoittaa seuraavissa tehtävissä laskulausekkeet näkyviin.
6. Laske
a) 13 % luvusta 375.
b) 17 % luvusta 157.
c) 3 % luvusta 748.
d) 69 % 780 eurosta.
e) 110 % 5,5 eurosta.
f) 137 % luvusta 245.
7. Kuinka monta prosenttia
a) 10 metriä on 16 metristä.
b) 400 grammaa on 2 kilogrammasta.
c) 48 minuuttia on tunnista.
d) 40 euroa on 120 eurosta.
e) 15 senttiä on 3 metristä.
f) 2,5 desilitraa on 2 litrasta.
8. Lukujärjestyksessä on viikossa yhteensä 30 tuntia opetusta, joista 4 h on matematiikkaa. Kuinka monta prosenttia viikon oppitunneista on matematiikkaa?
9. Tuotteen hinta on 680 euroa. Saat tuotteesta alennusta 35 %. Kuinka suuri alennus on euroina?
10. Karkkipussissa on suklaakarkkeja 31 %. Karkkeja on yhteensä 48 kappaletta. Kuinka monta suklaakarkkia pussissa on.
11. Kuinka monta prosenttia luku 1547 on luvusta 1655?
12. Kuinka monta prosenttia viikon päivistä on arkipäiviä?
13. Päättele, mistä määrästä
a) 50 % on 85 €
b) 10 % on 32
c) 25 % on 34 m
d) 20 % on 15 €
e) 100 % on 84
f) 150 % on 75 €
14. . Laske, mistä luvusta
a) 35 % on 25
b) 22 % on 457
c) 87 % on 48
d) 54,3 % on 1582
e) 97 % on 578
f) 111 % on 358.
g) 250 % on 1340
h) 0,2 % on 539
15. Televisio maksoi ennen joulua 499 € ja joulun jälkeen alennusmyynnissä 349 €. Mikä oli television alennusprosentti?
16. Kallen bruttopalkka oli 2540 € kuukaudessa. Kallen nettopalkka oli tältä kuukaudelta 2057 €. Kuinka monta prosenttia Kallen palkasta meni veroihin ja muihin maksuihin?
17. Ihmisessä on vettä noin 65 %. Kuinka monta kilogrammaa 60 kg:sta ihmisestä on vettä?
18. Rahoista jäi käyttämättä 43 % eli 1245 €. Kuinka paljon rahaa oli alun perin?
19. Karkkipussissa on 7 keltaista karkkia. Keltaisten karkkien osuus on 41,2 % koko karkkipussin karkeista. Kuinka monta karkkia pussissa on yhteensä?
20. Jogurtissa on hedelmää 6 %. Kuinka monta grammaa 150 g jogurttipurkista on hedelmää?
21. Meriveden suolapitoisuus on 3,5 %. Kuinka paljon merivettä oli alun perin, jos haihdutuksen jälkeen vedestä jäi jäljelle 21 g suolaa?
22. Marjaseos sisältää 27 % vadelmia ja loput mustikoita. Vadelmia on 1540 g.
a) Kuinka paljon marjaseosta on yhteensä?
b) Kuinka paljon on mustikoita?
23. Luokan oppilaista on poikia 60 %. Kuinka monta poikaa luokalla on, kun tyttöjä on 12?
Muutosprosentti, tehtävät
1. Minnan bruttopalkka oli 2695 € kuukaudessa. Minnan palkasta meni veroihin ja muihin maksuihin 22 %. Kuinka paljon Minnan nettopalkka oli?
2. Kirjan normaali hinta on 41,90 €. Kirja oli 20 prosentin alennuksessa. Kuinka paljon kirja maksoi alennuksen jälkeen?
3. Polkupyörän hinta oli talvella 345 €. Kevään tullen hintaa nostettiin 10 %. Kuinka paljon polkupyörä maksoi keväällä?
4. Eväsleipä maksoi kaupassa 3,90 €. Leivän parasta ennen -päiväys lähestyi ja leipä laitettiin 30 % alennukseen. Kuinka paljon leipä maksoi alennuksen jälkeen?
5. Vuonna 2019 Suomen väliluku oli 5 520 000. Vuonna 2000 suomen väkiluku oli 5 181 000. Kuinka monta prosenttia Suomen väliluku oli
a) pienempi vuonna 2000 kuin vuonna 2019?
b) suurempi vuonna 2019 kuin vuonna 2000?
6. Vuonna 2019 Suomen väkiluku oli 5 520 000 ja väestöstä 88,0 % puhui äidinkielenään suomena. Kuinka monta äidinkielenään suomea puhuvaa asukasta Suomessa oli?
7. Vuonna 2019 Helsingin väkiluku oli 648 040. Kuinka monta prosenttia Helsingin väkiluku oli koko Suomen väkiluvusta?
8. Tuotteen hintaa nostettiin 20 %, jolloin tuotteen uusi hinta oli 10,80 €. Mikä oli alkuperäinen hinta?
9. Tuote myytiin 20 % alennuksella hintaan 14,40 €. Mikä oli alentamaton alkuperäishinta?
10. Lapsi oli vuoden alussa 108 cm pitkä ja vuoden lopussa 113 cm pitkä. Kuinka paljon lapsi kasvoi vuoden aikana prosentteina?
11. Pertti juoksi Cooperin testissä keväällä 2050 m. Pertti harjoitteli kesän ahkeraksi ja juoksi elokuussa testissä 2390 m. Kuinka monta prosenttia Pertin tulos parantui?
12. Elokuussa 2019 Seinäjoella oli 63 600 asukasta. Jos asukasluku on seuraavana vuonna 64 100, kuinka paljon väestönkasvu on prosentteina?
13. Kenkien hinta oli alun perin 149 €. Kenkien hintaa alennettiin ensin 30 % ja tämän jälkeen vielä 10 %. Mikä oli kenkien hinta alennusten jälkeen?
14. Mansikoiden perkauksessa tulee hävikkiä 5 %. Mansikkahillo sisältää 65 % mansikkaa. Kuinka paljon perkaamattomia mansikoita tarvitaan, kun valmistetaan 1500 g mansikkahilloa?
15. Kauppias osti joulukoristepaketin hintaan 24,37 €. Kauppias myi joulukoristepaketin hintaan 35,90 €. Joulun jälkeen kauppias laittoi joulukoristepaketin 30 % alennukseen. Kuinka paljon kauppias sai voittoa prosentteina joulukoristepaketista
a) ennen joulua?
b) joulun jälkeen?
Peräkkäiset muutokset
Peräkkäisissä prosenttimuutoksissa muutos toistuu monta kertaa ja muutokset voivat olla joko lisäystä tai vähennystä.
Esimerkki 1: Tietokoneen hinta oli aluksi 600 euroa. Black Friday -kampanjan takia tuotteen hintaa alennettiin aluksi 60 % ja vielä uudestaan 60 % lisää. Mikä oli tietokoneen hinta alennuksien jälkeen?
Jos vain lopullinen hinta kaikkien muutosten jälkeen halutaan selvittää, saadaan muutosten jälkeinen hinta yhdistämällä lisäys- ja vähennyskertoimet.
Prosenttimuutoksia ei voida laskea yhteen, koska muuten alennuksen määrä olisi 120 %, mikä ei ole mahdollista. Peräkkäiset muutokset täytyy laskea kertomalla lisäys- tai vähennyskertoimet. Kun alennus on 60 %, jäljelle jää maksettavaksi 40 %, jolloin uusi hinta on:
$600\ €\cdot0{,}4\cdot0{,}4=96\ €$
Esimerkki 2: Lomamatkan hinta oli aluksi 680 euroa. Sen hinta nousi ensin 12 %, sitten se laski 7,5 % ja lopuksi vielä nousi 25 %. Mikä oli matkan hinta muutosten jälkeen?
$680\ €\cdot1{,}12\cdot0{,}925\cdot1{,}25=880{,}60\ €$
Huomaa, että korotuksessa prosenttimäärä lisätään 100 %, eli esimerkiksi 12 % hinnan nousu tarkoittaa, että uusi hinta on 112 % alkuperäisestä, eli 1,12-kertainen.
Joissain tapauksissa esimerkiksi tuotteen hinnasta tiedetään ainostaan muutos, mutta ei alkuperäistä tai lopullista hintaa. Tällaisessa tilanteessa lähtöarvoksi voi laittaa jonkun keksityn arvon, kuten 100. Alkuperäistä arvon voi myös merkitä tuntemattomaksi, eli esimerkiksi x:ksi.
Esimerkki 3: Keväällä erään matkailupalvelutuotteen hintaa korotetaan 30 % ja syksyllä alennetaan 28 %. Kuinka monta prosenttia syksyn hinta on alkuperäistä hintaa korkeampi tai alhaisempi?
Olkoon hinta aluksi 100 € (alkuperäinen hinta), jolloin syksyn hinta on:
$100 \ €\cdot1{,}3\cdot0{,}72=93{,}60\ €$
Jolloin hinnan erotus
$93{,}60\ € - 100 \ € = - 6{,}4\ €$
Prosenttimuutos:
$\frac{-6{,}4\ €}{100\ €}\cdot100\ \%\ =\ -6{,}4\ \%$
Tehtävät
Prosenttiyksikkö ja promille, tehtävät
Prosenttiyksikkö
1. Joulukuun alussa 2019 kokoomuksen kannatus oli 18,6 %. Perussuomalaisten kannatus oli 5,7 prosenttiyksikköä korkeampi. Kuinka paljon oli perussuomalaisten kannatusprosentti?
2. Joulukuun alussa 2019 keskustan kannatus oli laskenut 2,3 prosenttiyksikköä ja oli nyt 10,6 %. Kuinka monta prosenttia kannatus oli laskenut?
3. Ammatillisen tutkinnon keskeyttäneiden osuus oli noussut kolmessa vuodessa 8,6 prosentista 11,4 prosenttiin (2017). Kuinka paljon keskeyttämisten nousu on
a) prosenttiyksikköinä?
b) prosentteina?
4. Suomen työttömyysaste oli vuoden 2018 tammikuussa 8,8 % ja vuoden 2019 tammikuussa 6,8 %.
a) Kuinka monta prosenttiyksikköä työttömyysaste laski?
b) Kuinka monta prosenttia työttömyysaste laski?
c) Kuinka paljon Suomessa oli työikäisiä vuoden 2019 tammikuussa, kun työttömiä oli 169 000?
5. 340:stä opiskelijasta elokuussa 254 opiskelijaa näki teatteriesityksen. Lokakuussa 287 opiskelijaa näki esityksen. Kuinka monta opiskelijaa enemmän näki esityksen lokakuussa kuin elokuussa
a) prosentteina?
b) prosenttiyksikköinä?
6. Katrin veroprosentti nousi 22,0:sta 22,8:aan prosenttiin. a) Ilmoita veroprosentin nousu prosentteina ja prosenttiyksikköinä. b) Kuinka paljon Katrin bruttopalkka oli vuodessa, jos veroihin meni vuodessa 8550 € ja veroprosentti oli 22,8?
7. Vuoden 2015 eduskuntavaaleissa SDP sai 34 paikkaa ja vuoden 2019 eduskuntavaaleissa 40 paikkaa. Eduskuntaan valitaan aina 200 kansanedustajaa. a) Kuinka monta prosenttia SDP sai paikoista vuonna 2015 ja vuonna 2019? b) Kuinka monta prosenttia enemmän SDP sai paikkoja vuonna 2019 kuin vuonna 2015? c) Kuinka monta prosenttiyksikkö enemmän SDP sai paikkoja vuonna 2019 kuin vuonna 2015?
8. Vuonna 2019 asuntolainan koroista voidaan vähentää vielä 25 % verotuksessa. Vuoden 2020 alusta vähennysoikeus laskee 10 prosenttiyksikköä. Jos asuntolainaa on 55 000 € ja lainan korkokanta on 1,10 % (ja lainaa ei lyhennetä vuoden mittaan), kuinka paljon asuntolainan vähennysoikeus on
a) vuoden 2019 verotuksessa?
b) vuoden 2020 verotuksessa?
Promille
9. Täydennä taulukko.
| Promille, ‰ | Prosentti, % | Desimaaliluku |
|---|---|---|
| 0,2 | ||
| 5 | ||
| 0,035 | ||
| 3,7 | ||
| 0,4 |
10. Kultakorussa on promilleleima 750. Promilleleima tarkoittaa, että korusta 750 ‰ on kultaa. Jos kultakorun massa on 2450 mg, kuinka paljon korusta on puhdasta kultaa?
100 % kulta on suhteellisen pehmeää, joten siksi kultakorut eivät ole 100 % kultaa. Kultakorut ovat kultaseoksia, joissa seosaineena käytetään mm. hopeaa, kuparia ja sinkkiä. Seosaine tekee koruista kovempia sekä muuttaa kultakorun väriä.
11. Hopeakorun massa on 4,50 g ja korusta on puhdasta hopeaa 4,16 g. Mikä promilleleima (vastaavasti kuin kultakoruissa) hopeakorussa on?
12. Kultapitoisuus voidaan ilmaista myös karaatteina. Jos kulta on puhdasta kultaa (100 %) karaatteja on 24. Suomessa yleisin kultapitoisuus on 14 karaattia (14k). Tällöin kullasta $\frac{14}{24}$ on kultaa. Jos kultapitoisuus on 14 karaattia, kuinka monta promillea tällöin korussa on kultaa?
13. Rattijuopumuksen raja on 0,5 ‰ ja törkeän rattijuopumuksen raja on 1,2 ‰. Ylittyykö rattijuopumuksen tai törkeän rattijuopumuksen raja, jos veressä on alkoholi 3500 mg ja verta on kyseisessä ihmisessä 5,0 kg?
14. Junaradan pituuskaltevuus saa olla korkeintaan 15 promillea eli junaraide saa nousta korkeintaan 15 ‰. Kuinka paljon junarata saa korkeintaan nousta 550 metrin matkalla?
15. Huopalahti-Vantaankoski -välillä junaradan pituuskaltevuus on poikkeusluvalla 22,5 ‰ kalteva. Kuinka paljon junarata nousee tällöin 550 metrin matkalla?
16. Kuinka paljon on pituuskaltevuus promilleina, jos junarata laskee 2,5 km matkalla 32 500 mm?
17. Noin yhdellä promillella suomalaisista jää kehittymättä kuusi tai useampi pysyvistä hampaista (oligodontia). Jos kaupungin asukasluku on 50 000, kuinka monella kaupunkilaisella voidaan odottaa olevan oligodontia?
18. Vuoden 2017 aikana muuttovoitto oli Uudellamaalla 9,1 ‰ eli 15 043 henkilöä. Kuinka paljon Uudellamaalla oli asukkaita vuoden 2017 alussa tämän mukaan?
19. Alkoholijuoman etanoli jakautuu tasaisesti koko elimistön nestemäärään (veri + muut nesteet). Yleensä kehon alkoholipitoisuus ilmoitetaan kuitenkin veren alkoholipitoisuutena, koska alkoholipitoisuus mitataan verestä. Miehen kehon nestemäärä on noin 75 % ruumiinpainosta ja naisen noin 66 % ruumiinpainosta.
70 kg painava mies juo 3 pulloa keskiolutta (tilavuus 0,33 l ja 4,5 % alkoholia) nopeasti. Mikä on veren alkoholipitoisuus?