meta data for this page
Kolmio
Kolmiossa on kolme sivua ja kolme kulmaa. Kolmion kulmien summa on yhteensä 180° eli kun kolmiot kulmat lasketaan yhteen, tulos on 180°. Kolmiot voidaan luokitella kahdella tapaa: sivujen perusteella ja kulmien perusteella.
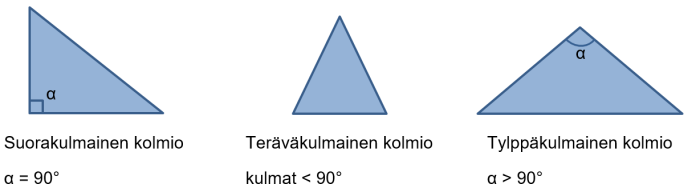
Kolmioiden luokittelu kulmien mukaan
Suorakulmaisessa kolmiossa on yksi suora kulma eli kulman suuruus on 90°. Kaksi muuta kulmaa ovat alle 90 astetta. Suoran kulman merkintänä käytetään pientä neliötä suorassa kulmassa eli tasan 90° kulmassa, muut kulmat merkitään kaarella. Suorakulmaisesta kolmiosta voidaan laskea sivujen pituuksia Pythagoraan lauseen avulla tai sivujen ja kulmien suuruuksia trigonometristen funktioiden avulla (sin, cos, tan).
Teräväkulmaisessa kolmiossa kaikkien kulmien suuruus on alle 90°.
Tylppäkulmaisessa kolmiossa yhden kulman suuruus on yli 90°. Tylppäkulmaisen kolmion kaksi muuta kulmaa ovat alle 90 astetta.
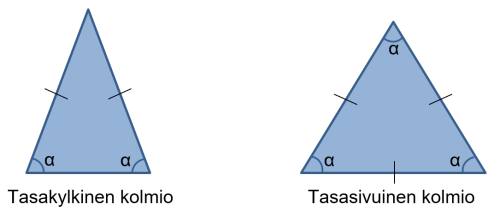
Kolmioiden luokittelu sivujen mukaan
Tasakylkisessä kolmiossa on kaksi yhtä pitkää sivua, jotka on merkitty kuvaan sivun keskellä olevilla pienillä viivoilla. Koska nämä kaksi sivua ovat yhtä pitkä, myös kolmion kantakulmat ovat yhtä suuret.
Tasasivuisessa kolmiossa kaikki sivut ovat yhtä pitkiä. Koska kaikki sivut ovat yhtä pitkiä, ovat kaikki kulmat myös yhtä suuria. Tasasivuisen kolmion yhden kulman suuruus on ${\frac{180°}{3}=60°}$.
Kolmion piiri ja pinta-ala
Kaksiulotteisille kappaleille lasketaan usein piiri ja pinta-ala.
Piiri tarkoittaa kaksiulotteisen kappaleen ympärysmittaa eli sitä matkaa, kun kierretään kappale ulkoreunoja pitkin ympäri ja palataan takaisin aloituspisteeseen. Piiri lasketaan sivujen pituuksien summana eli lasketaan kaikkien sivujen pituudet yhteen.
Kolmion piiri = sivun a pituus + sivun b pituus + sivun c pituus eli ${p=a+b+c}$, kun sivujen pituudet ovat a, b, ja c.
Pinta-ala tarkoittaa kaksiulotteisen kappaleen pinnan kokoa. Esimerkiksi jos ostetaan maalia seinän maalaamiseen, tarvitaan maalin ostoon tieto seinän pinta-alasta. Talon koko ilmoitetaan aina pinta-alana. Erilaisten kappaleiden pinta-alat lasketaan eri tavalla. Kolmion, nelikulmion ja ympyrän pinta-alojen laskukaavat täytyy osata ulkoa.
${kolmion\ pinta-ala=\frac{kanta\cdot korkeus}{2}}$ eli ${A=\frac{a\cdot h}{2}}$
Pinta-alan laskussa kanta ja korkeus ovat keskenään kohtisuorassa eli kantasivun ja korkeuden välille muodostuu 90 asteen kulma.
Kolmion piiri ja pinta-ala
${p=a\ +b\ +c}$
${A=\frac{a\cdot h}{2}}$
Esimerkkejä
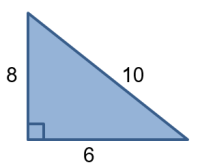
Kuvan kolmiossa on yksi 90 asteen kulma eli kolmio on suorakulmainen kolmio.
Kolmion piiri: ${p=6+8+10=24}$
Kolmion pinta-ala: ${kolmion\ pinta-ala=\frac{6\cdot8}{2}=24}$
Tässä tehtävässä on sattumaa, että piirin ja pinta-alan lukuarvo on sama - yleensä näin ei ole.
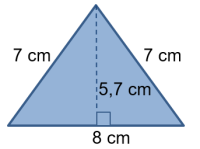
Kuvan kolmiossa on kaksi yhtä pitkää sivua (7 cm) eli kolmio on sivujen perusteella tasakylkinen kolmio.
Silmämääräisesti näyttää siltä, että kolmion kaikki kulmat ovat alle 90° eli kolmio on kulmien perusteella teräväkulmainen kolmio.
Kolmion piiri: ${p=8\ cm+7\ cm+7\ cm\ =22\ cm}$
Kolmion pinta-ala: ${A=\frac{8\ cm\cdot5{,}7\ cm}{2}=22{,}8\ cm^2}$
Huomaa piirin ja pinta-alan yksiköt. Piiri on matka eli sen perusyksikkö on metri. Pinta-alan perusyksikkö on neliömetri, ${m^2}$.