meta data for this page
Ympyrä
- Ympyrä on kaksiulotteinen kappale, samoin kuin kolmio, nelikulmiot ja monikulmiot.
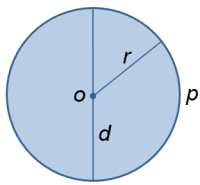
- Ympyrään liittyvät käsitteet halkaisija (d), säde (r), piiri (p) eli kehä ja keskipiste (o).
- Säde on jana, joka kulkee ympyrän keskipisteestä kehälle.
- Säteitä voidaan piirtää ympyrään ääretön määrä. Jokainen samalle ympyrälle piirretty säde on yhtä pitkä.
- Halkaisija on jana, joka kulkee keskipisteen kautta ympyrän kehältä kehälle.
- Halkaisija on kaksi kertaa säteen pituus eli ${d=2\cdot r}$.
Ympyrä
${d=\text{halkaisija}}$
${r=\text{säde}}$
${p=\text{piiri eli kehä}}$
${o=\text{keskipiste}}$
Esimerkkejä
Esim. 1. Laske ympyrän halkaisija, kun ympyrän säde on 5 cm.
${d=2\cdot r=2\cdot 5\ cm=10\ cm}$
Esim. 2. Laske ympyrän säde, kun ympyrän halkaisija on 1 m.
${r=\frac{d}{2}=\frac{1\ m}{2}=0{,}5\ m=50\ cm}$
Ympyrän piiri ja pinta-ala
Ympyrän piirin ja pinta-alan laskemiseen tarvitaan vakiota pii. Piin merkki on π ja sen likiarvo on 3,14. Laskutehtävissä kannattaa kuitenkin käyttää laskimestä löytyvää π-näppäintä, jolloin piin arvo saadaan paljon tarkemmin. Todellisuudessa π:n desimaalit eivät pääty koskaan, eli π on päättymätön desimaaliluku.
Ympyrän piiri ja pinta-ala
${p=π\cdot d=π\cdot 2\cdot r}$
${A=π\cdot r^2=π\cdot r\cdot r}$
Esim. 3. Laske ympyrän piiri ja pinta-ala, kun ympyrän säde on 8 cm.
${r=8\ cm}$
Ympyrän halkaisija saadaan laskettua ympyrän säteen avulla, eli
${d=2\cdot r=2\cdot 8\ cm=16\ cm}$
Piiri voidaan laskea kertomalla ympyrän halkaisija π:llä.
${p=π\cdot 16\ cm=50{,}27\ cm≈50\ cm}$
Ympyrän pinta-ala voidaan laskea säteen ja π:n avulla:
${A=π\cdot r^2=π\cdot \left(8\ cm\right)^2=201\ cm^2≈200\ cm^2}$