meta data for this page
Tilastojen esittäminen
Tilastollinen jakauma ilmoittaa kaikki havaintoarvot, sen kuinka yleinen kukin havaintoarvo on. Havaintoarvojen esiintymistä eli lukumäärää kutsutaan frevenssiksi. Alla on taulukko, jossa opiskelijoiden lempiharrastusta kysyttiin
| Lempiharrastus | Frekvenssi |
| Jalkapallo | 10 |
| Jääkiekko | 8 |
| Luistelu | 5 |
| Kuntosali | 16 |
Kertauksena: havaintoarvo on lempiharrastukset, eli jalkapallo, jääkiekko, luistelu sekä kuntosali. Frekvenssi ilmoittaa, kuinka moni opiskelija ilmoitti pitävänsä kyseisestä urheilulajista. Esimerkiksi jalkapalloa piti 10 opiskelijaa lempiharrastuksena.
Frekvenssit ilmaistaan usein erilaisten kaavioiden avulla. Tyypillisiä kaavioita ovat pylväsdiagrammit sekä histogrammit.
Pylväsdiagrammi
- Pylväsdiagrammissa vaaka-akselilla (x-akselilla) on muuttuja
- Pylväsdiagrammissa pystyakselilla (y-akselilla) on frekvenssin lukumäärä
- Pylväsdiagrammi soveltuu parhaiten epäjatkuville muuttujille, koska palkit ovat erillään toisistaan
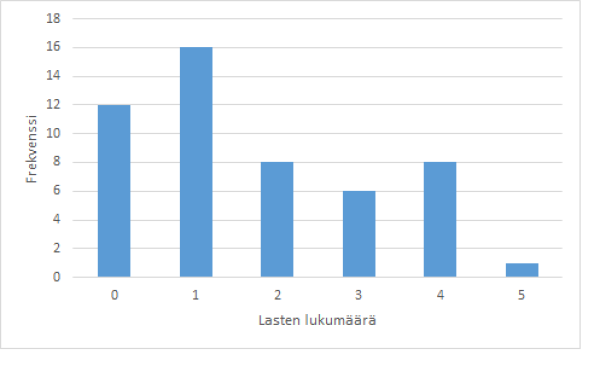
Laaditaan alla olevalle aineistolle pylväsdiagrammi
| Lasten lukumäärä | Frekvenssi |
| 0 | 12 |
| 1 | 16 |
| 2 | 8 |
| 3 | 6 |
| 4 | 8 |
| 5 | 1 |
Koska lasten lukumäärä saa vain tiettyjä arvo, on kyseessä epäjatkuva muuttuja. Asetetaan x-akselille lasten lukumäärät (0-5) ja y-akselilla jokaista lasten lukumäärää vastaava frekvenssi eli havaintojen lukumäärä. Saadaan alla oleva kuvaaja
Histogrammi
- Histogrammi poikkeaa pylväsdiagrammista siten, että palkit ovat kiinni toisissaan
- Histogrammi voidaan piirtää ainoastaan jatkuville muuttujille, jotka voivat saada siis mitä vain arvoja tietyltä väliltä
- Jatkuville muuttujille ei voida piirtää pylväsdiagrammia, koska tällöin muodostuisi tyhjiä kohtia, joita jatkuvissa muuttujissa ei ole
- Histogrammissa on tyypillisesti siis erilaisia luokkia x-akselilla
Laaditaan alla olevalle aineistolle histogrammi
| Halkojen pituus | Frekvenssi |
| 20-24 | 5 |
| 25-29 | 10 |
| 30-34 | 26 |
| 35-39 | 21 |
| 40-44 | 8 |
| 45-49 | 2 |
Halkojen pituus saa siis mitä tahansa arvoja, tässä tapauksessa väliltä 20-49. Laaditaan aineistosta histogrammi. 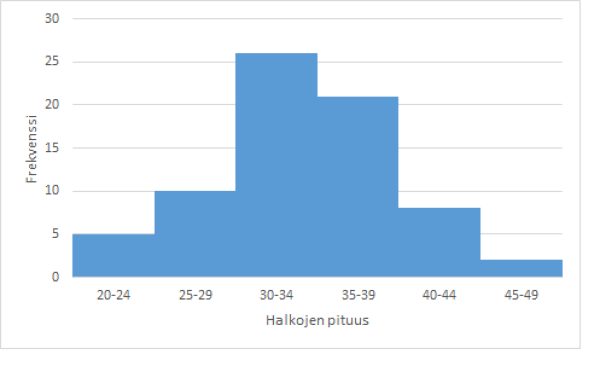
Viivadiagrammi
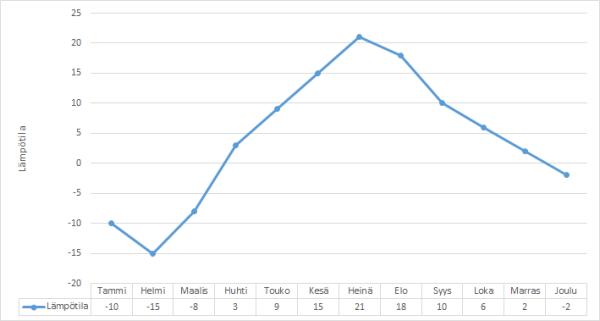
Viivadiagrammeja käytetään havainnollistamaan ajan mukana muuttuvien ilmiöiden eli aikasarjojen graafista esittämistä. Viivadiagrammin tarkoitus on kertoa lukijalle, mihin suuntaan ja kuinka nopeasti tutkittava ilmiö kehittyy. Alla on esimerkki vuoden aikana kuukauden keskilämpötiloista.
Ympyrädiagrammi
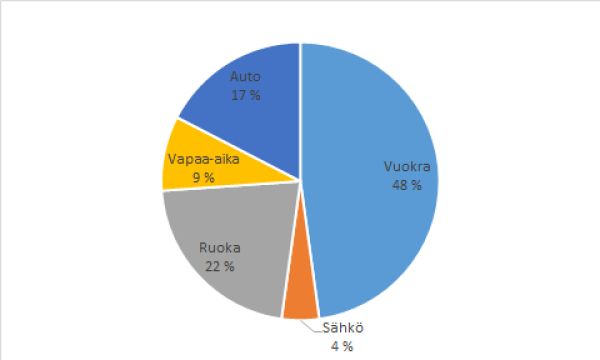
Ympyrä- eli sektoridiagrammeja käyetään havainnollistamaan kokonaisuuden jakautumista osioon. Tavallisesti nämä osuudet ilmaistaan prosenttilukuina. Ympyrädiagrammissa havaitaan siis usein erilaisia muuttujatyyppejä. Alla on esimerkki kuukauden aikana olevien kulujen jakautuminen.