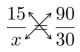meta data for this page
Verrannollisuus
Kahden murtoluvun yhtälöä kutsutaan verrannoksi. Näiden ratkaisulla on paljon hyödyllisiä sovelluksia matematiikassa. Verrantojen hallitsemisesta on paljon hyötyä mm. prosenttilaskuissa.
Esim. 1.
Miten ratkaiset yhtälön $\frac{15}{x} = \frac{90}{30}$
Yhtälö voidaan ratkaista kertomalla luvut ristiin. Vasemman puolen nimittäjä kerrotaan oikean puolen osoittajalla, ja vasemman puolen osoittaja kerrotaan oikean puolen nimittäjällä.
$x\cdot 90 = 15\cdot 30$
$x = \frac{15\cdot 30}{90} = 5$
Vastaus: $x =5$
Esim. 2.
Miten ratkaiset yhtälön $\frac{3x}{27} = \frac{5}{15}$
Kertomalla yhtälö ristiin, saadaan
$3x\cdot 15 = 27\cdot 5$
$45x = 135$
$x = \frac{135}{45}$
$x = 3$
Esim. 3
Pääset pyörällä 34 kilometrin matkan kahdessa tunnissa. Kauanko kestää samalla nopeudella 25 kilometrin matkassa?
Verranto voidaan ratkaista helpoiten tekemällä taulukko:
| Matka (km) | Aika (h) |
|---|---|
| 34 | 2 |
| 25 | x |
Kyseessä on suoraan verrannollisuus eli kun matka kasvaa, aika lisääntyy. Tässä tehtävässä matka vähenee, niin aika vähenee.
Muodostetaan taulukosta yhtälö, jossa numeroiden ja x:n paikka pysyvät samoina:
$\frac{34}{25} = \frac{2}{x}$
Ratkaistaan yhtälö x:n suhteen:
$34\cdot x = 25\cdot 2$
$34x = 50$
$x = \frac{50}{34} = 1,47$
eli 1,47 h.
0,47 tuntia on minuutteina:
$ 0,47\cdot 60 \min = 28 \min\ $
Vastaus: $ 1\ \mathrm{h} \ 28\ \mathrm{min} $