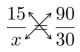meta data for this page
Mittakaava
Mittakaavaa käytetään, kun halutaan ilmoittaa todellisen koon ja siitä tehdyn pienoismallin suhde. Esimerkiksi maastokartta on aina pienoismalli luonnosta. Kartassa tuleekin aina ilmoittaa käytetty mittakaava. Mittakaava kertoo, paljonko karttaa on pienennetty todellisesta.
Mittakaava 1:200 tarkoittaa pienennystä, jossa 1 mittayksikkö pienoismallissa vastaa 200 mittayksikköä luonnossa. Jos esimerkiksi kuvan laivan pienoismalli on 0,10 metrin pituinen, on todellinen laivan koko 200-kertainen, eli 20 metriä.
Miten lasketaan?
Esim. 1.
Miten ratkaiset oheisen yhtälön? $\frac{15}{x} = \frac{90}{30}$
Yhtälö voidaan ratkaista kertomalla luvut ristiin. Vasemman puolen nimittäjä kerrotaan oikean puolen osoittajalla, ja vasemman puolen osoittaja kerrotaan oikean puolen nimittäjällä.
$x\cdot 90 = 15\cdot 30$
$x = \frac{15\cdot 30}{90} = 5$
Vastaus: $x =5$
Esim. 2.
Talon pohjapiirustuksessa mittakaava on 1 : 100. Piirustuksessa olohuhuoneen leveys on 3 cm. Kuinka leveä olohuone on todellisuudessa?
Mittakaavatehtävät voi ratkaista helpoiten tekemällä taulukko:
| Mittakaava | Koko (cm) | |
|---|---|---|
| Kuvassa | 1 | 3 |
| Luonnossa | 100 | x |
Tehdään ylläolevista luvuista verrantoyhtälö ja ratkaistaan se ristiinkertomalla.
$\frac{1}{100}=\frac{3}{x}$
$1\cdot x=3\cdot100$
$x=300$
Vastauksen yksikkö on sama kuin lähtötiedoissa, eli vastaus on $\boldsymbol{300\ cm}$.
Esim. 3.
Suunnistuskartan mittakaava on 1 : 10 000. Kuinka pitkää matkaa kartalla vastaa 100 m luonnossa?
Tehdään taulukko vastaavasti kuin edellisessäkin esimerkissä, mutta nyt yksikkönä on metri.
| Mittakaava | Koko (m) | |
|---|---|---|
| Kartalla | 1 | x |
| Luonnossa | 10 000 | 100 |
Tehdään verrantoyhtälö ja ratkaistaan se ristiinkertomalla.
$\frac{1}{10000}=\frac{x}{100}$
$x \cdot 10000=100\cdot 1$
$x= \frac{100}{10000}=0,01$
Yksikkö on sama kuin lähtöarvoissa, eli metri. Vastaus on siis $\boldsymbol{0,01\ m = 1\ cm}$.
Esim. 4.
Pienessä Suomen kartassa Suomen korkeus on 11 cm. Todellisuudessa Suomen korkeus on noin 1100 km. Mikä on kartan mittakaava?
Ennen taulukon tekemistä muutetaan annetut suureet samaan yksikköön. Molemmat voi muuttaa esimerkiksi metreiksi.
$11\ cm = 0,11\ m$
$1\ 100\ km = 1\ 100\ 000\ m$
Syötetään saadut luvut taulukkoon. Koska emme tiedä mittakaavaa, käytetään mittakaavana 1 : x.
| Mittakaava | Koko (m) | |
|---|---|---|
| Kartalla | 1 | 0,11 |
| Luonnossa | x | 1 100 000 |
Ratkaistaan x.
$\frac{1}{x} = \frac{0,11}{1\ 100\ 000}$
$x\cdot 0,11 = 1\cdot 1\ 100\ 000$
$x = \frac{1\cdot 1\ 100\ 000}{0,11} = 10\ 000\ 000$
Vastaus: Kartan mittakaava on $\boldsymbol{1:10\ 000\ 000}$.